5 LASSO
複雑なモデルを適切に推定する方法として、LASSO (Tibshirani 1996) を紹介します。 LASSOは、罰則付き回帰と呼ばれる枠組みの一つの手法です1。 OLSと同様に線型予測モデルを推定しますが、データへの当てはまりだけでなく、モデルの複雑性も抑制することも目指します。
5.1 推定方法
例として、以下のモデルの推定を目指します。\[\beta_1 Size\times 板橋区ダミー+.. + \beta_6 Size^6\times 板橋区ダミー\] \[+..+\beta_{132} Size\times 中央区ダミー+.. +\beta_{138} Size^6\times 中央区ダミー\]
合計138個のパラメタがあり、事例数次第では、OLSによる推定は困難です。 これはOLS推定が、以下を最小化するように\(\beta\)を推定しているためです。 \[(Y - モデルの値)^2 のデータ上の平均\] \(\beta\)の数が多いと、データへの不適合度をいくらでも低下させられるため、複雑なモデルを推定するとデータへの過剰な適合 (母平均からの乖離)を引き起こします。
LASSO推定では、\(\beta\) の値を以下を最小化するように決定します。
\[(Y - 予測値)^2 のデータ上の平均\] \[+ \underbrace{\lambda}_{Tunning\ Parameter}\times (\beta_1の絶対値 +\beta_2の絶対値+..)\] \(\lambda\)は、データではなく、母平均への当てはまりを高めるように決定する。 具体的には、交差検証を用いる方法(Tibshirani 1996)、情報基準などの理論的な評価指標を用いる方法などがある (Belloni, Chernozhukov, and Hansen 2014; Taddy 2017) 。
\(\lambda\) に応じて、予測モデルがどのように変化するのか考えてみます。 \(\lambda\) を変化させることで、予測モデルは、単純平均と複雑なモデルのOLSの間で変化することになります。 \(\lambda=0\) であれば、OLSと全く同じモデルを推定します。 よって複雑な線型モデルを推定した場合は、データ上の平均値に近いモデルとなります。 \(\lambda\) を非常に大きい値を設定した場合、\(\beta_1=\beta_2=..= 0\) となります。 この場合は\(\beta_0\)をデータに当てはまるように推定することになります。
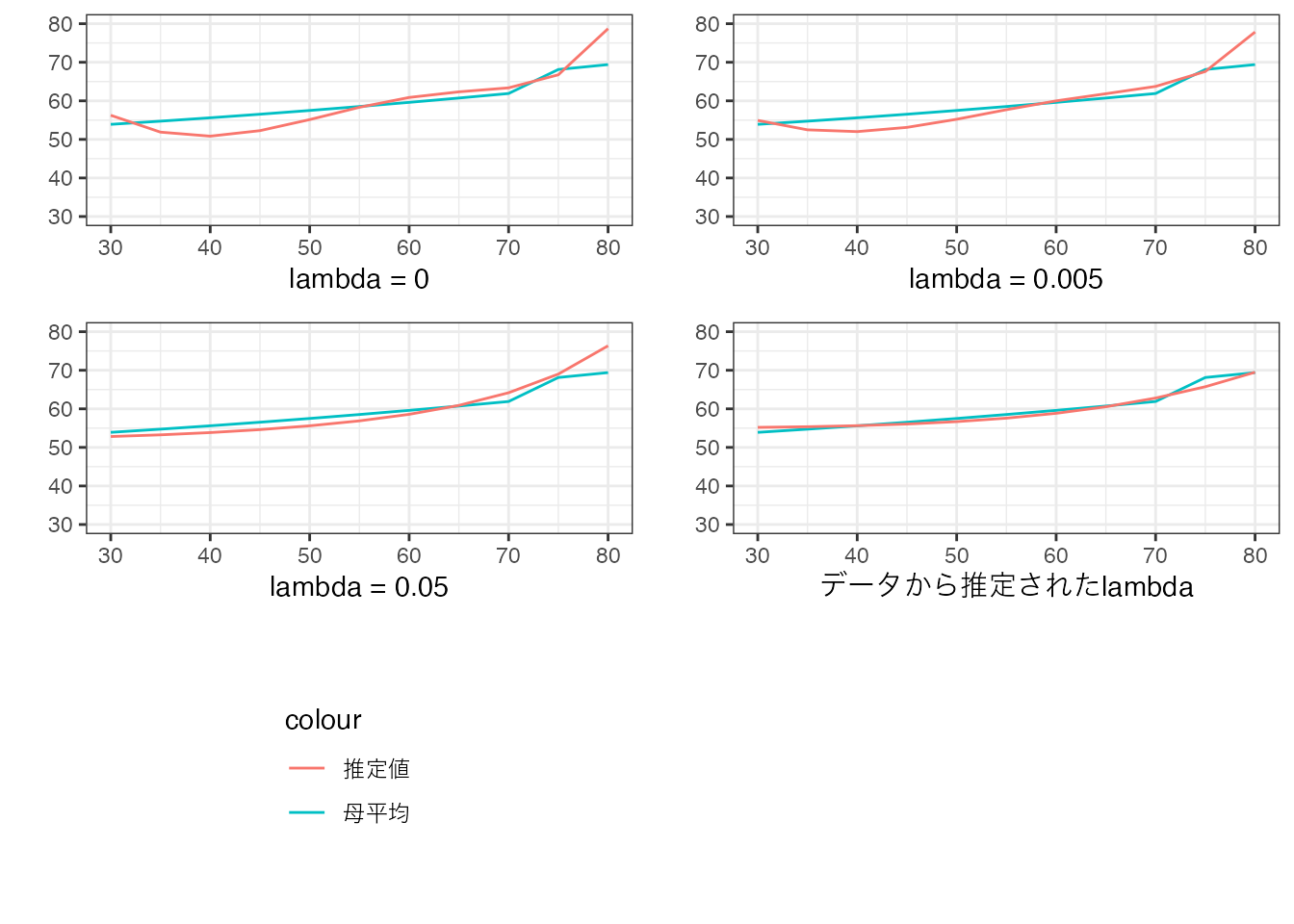
以下の数値例は、200事例からなるデータについて、LASSOにより以下のモデルを推定しました \[\beta_0 + \beta_1Size+..+\beta_6Size^6\]
\(\lambda\)については、0,0.005,0.05、および赤池情報基準により選ばれた値 (Taddy 2017) を使用した結果を図示しています。
母平均を青線、LASSOによる推定結果を赤線で示しています。
\(\lambda=0\) に比べると、\(\lambda\) の値が大きくなるにつれ、モデルが単純な曲線に近づいていることが確認できます。 また Taddy (2017) に基づいて設定された\(\lambda\) のもとでは、かなり単純化されたモデルが推定されたことも確認できます。
\(\lambda\) は、\(\beta\) と異なり、データへの当てはまりを最大化するように決定できません。 なぜでしょうか?
5.1.1 事例数の拡大
推定結果は、一般に事例数に強く影響を受けます。 特にLASSOなどの機械学習の方法においては、データの特徴により強く依存します。
以下の数値例では、事例数を100事例から1000事例まで増やし、 \(Y\sim Size + .. + Size^{10}\) をLASSOで推定しています (\(\lambda\) は Taddy (2017) の方法で設定しています)。
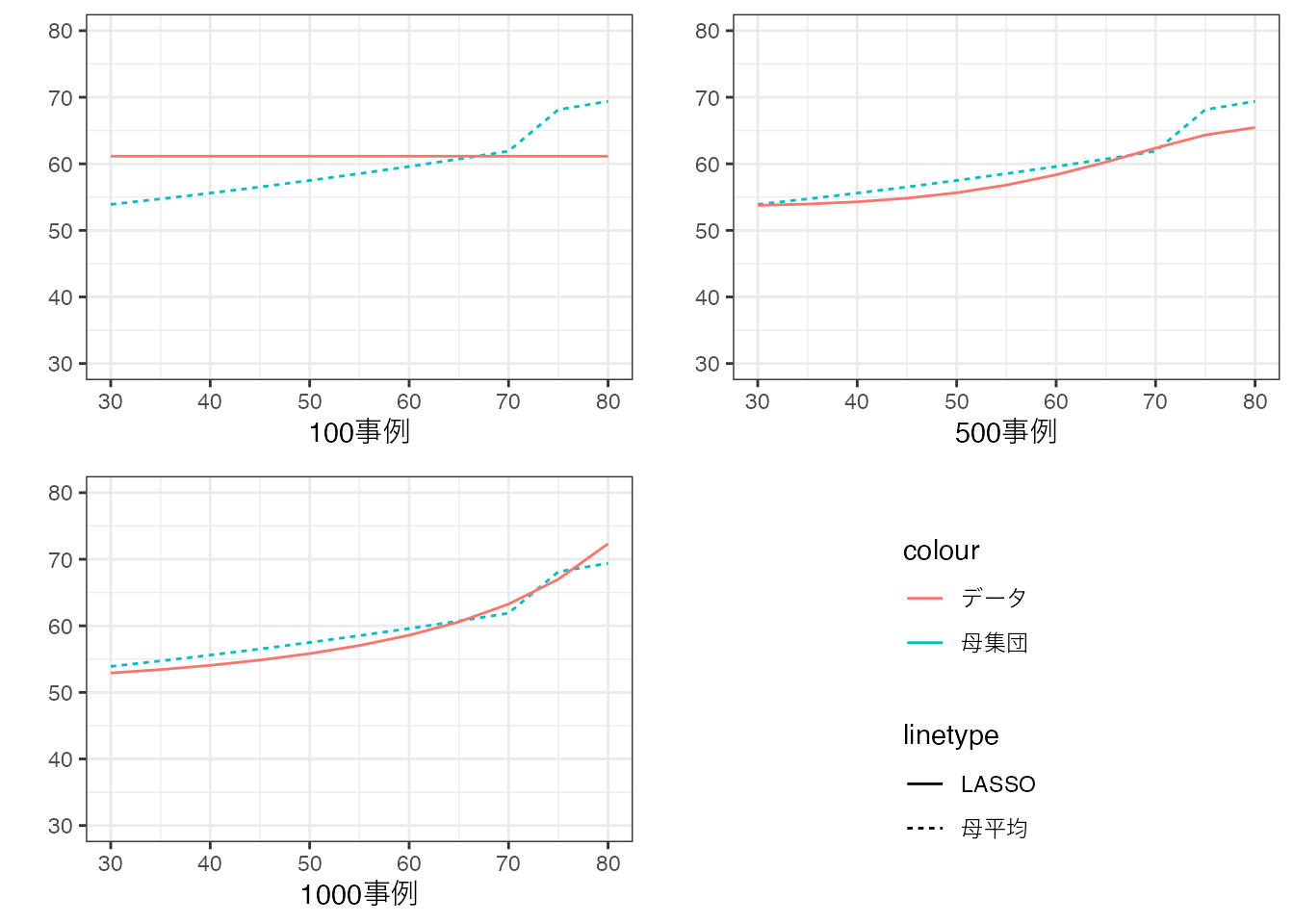
事例数の増加とともに、モデルの複雑性が、「自動調整」されていることが確認できます。 100事例では、単純平均値が推定されており、極めて単純なモデルが採用されています。 事例が増えると、モデルの傾きに加えて、「曲がり方」も変化しており、モデルが複雑化しています。
5.2 信頼区間
LASSOによって推定されたパラメタについて、信頼区間を計算する方法は盛んに議論されているものの、筆者の知る限り、現状確立された方法は存在しません2。
これはLASSO以外の「機械学習」の手法についても同様です。 一般にデータと推定値との関係性は、伝統的な推定方法と比べて、機械学習の方が複雑になります。 このため、理論的な関係性を導くのが難しく、信頼区間の計算方法の確率が困難となっています。
5.3 Rによる実践例
以下のパッケージを使用
readr (tidyverseに同梱): データの読み込み
gamlr: LASSO
Data = readr::read_csv("Public.csv") # データ読み込み
X = model.matrix(
~ 0 +
(Size + Tenure + StationDistance)**2 + # 交差項
I(Size^2) + I(Tenure^2) + I(StationDistance^2), # 二乗項
Data
) # X の作成
X = scale(X) # 標準化
colnames(X) # Xに格納されている変数の確認[1] "Size" "Tenure" "StationDistance"
[4] "I(Size^2)" "I(Tenure^2)" "I(StationDistance^2)"
[7] "Size:Tenure" "Size:StationDistance" "Tenure:StationDistance"合計101個のパラメタ推定を目指します。
gamlrパッケージ内のgamlr関数を用いてLASSO推定をします。
LASSO = gamlr::gamlr(
y = Data$Price, # Yの指定
x = X
) # LASSO推定推定された値は、以下で示します。 “.”は、厳密に0であることを意味しています。
coef(LASSO) # 推定値10 x 1 sparse Matrix of class "dgCMatrix"
seg100
intercept 42.705221
Size 18.372025
Tenure -4.476390
StationDistance .
I(Size^2) 15.265756
I(Tenure^2) 4.298650
I(StationDistance^2) .
Size:Tenure -11.614116
Size:StationDistance -9.213740
Tenure:StationDistance 1.656115