| Price | Size | LargeDistrict |
|---|---|---|
| 200 | 105 | 中心6区 |
| 150 | 105 | 中心6区 |
| 92 | 105 | 中心6区 |
| 110 | 105 | 中心6区 |
1 要約モデルの基本コンセプト
OLSや機械学習の代表的手法は、データが持つ特徴を要約するモデルを推定します。 要約は、データ分析における中核的アイディアであり、その重要性の理解が分析の第一歩となります。 まず本章では、要約の重要性を論じます。
1.1 観察できない変数が引き起こす問題
社会/市場分析における要約の必要性は、データから観察できない変数の存在にあります。 データから観察できない変数の存在は、あらゆる事例分析の最も深刻な問題の一つです。 このような変数への対処について、膨大な議論が蓄積されています。
観察できない変数がもたらす問題は、個別事例分析において特に顕著です。 以下では、取引価格(Price; 単位 \(=\) 100万円) と物件の特徴を、事例分析から考察していきます。
例えば、2億円で取引されている物件が、データの中に含まれていました。 この物件の広さ(Size)は105平米であり、中心6区(港区、千代田区、中央区、新宿区、渋谷区、文京区)に立地(District)してました。 この事例から、部屋の広さ(Size)が105平米で中心6区に立地している物件は、2億円で取引される傾向がある結論づけても良いでしょうか? ほとんどの応用でこのような推論は、不適切です。
実際に同じデータの中に、取引価格以外について、全く同じ特徴を持つ物件の取引事例が、3件ありました。 これらの4事例を比較すると、2億円はかなり高い価格での取引だったことがわかります。
なぜこのような取引価格のブレが生じるのでしょうか? データの誤入力など潜在的な理由は複数ありますが、有力なのはこのデータに含まれない重要な変数 が存在することです。 例えば、より詳細な立地(町丁目)、最寄駅や公園の近くに立地するか否かなども、価格決定において重要であると予想されます。 または売り手や買い手の”交渉力”など、属人的な属性も反映している可能性もあります。 このように、多様な要因が取引価格に影響を与え、結果として取引価格の下振れ/上振れが生じます。 しかしながら、このような変数は、データに含まれていません。
観察できない変数は不動産のみならず、個人や家計、企業、あるいは国レベルの分析でも同様の問題を引き起こします。 観察できる変数 \(X=[X_1,..]\) が一致した事例内でも、観察できない変数は事例間で異る可能性が高く、\(Y\) の値に大きな差が生まれます。
そして現実の社会や市場の複雑さを考慮すると、どれだけ詳細な調査を行ったとしても、\(Y\)に影響を与える全ての要因を観察することは困難です。
1.2 コンセプト: 集計
先の個別事例分析では、観察できない変数の偏りを確認する方法として、同じ\(X\)を持つ事例との整合性を確認しました。 このようなアプローチの発展として、同じ\(X\)を持つ事例集団について、\(Y\)の特徴を要約する方法があります。 例えば、平均値や分散、中央値、あるいは研究者による”所見”や”印象”、代表的な事例を紹介するなどです。
恣意的な分析を避けるためには、調査計画を立てる時点で、要約方法も決定し、分析を通じてコミットすることが重要です。 分析内で、どのような「指標」を使用するのか、分析を開始する前に決定することが望まれます。
このような要件を満たす指標として、代表的なものは平均値です。
\[\frac{Y_1 + .. + Y_N}{N}\]
ただし \(Y_i\) は第\(i\)事例の値、 \(N\) は事例数を表す。
以下では例として、価格 (Price) と広さ (Size)について、データに含まれる事例の分布をHeat mapで図示し、その後平均値を示します。

上記のHeat mapは、極めて乱雑であり、同じ\(X=Size\) でも \(Y=Price\) が異なる事例が多くなっています。 これは、顕著な観察できない変数の影響を示唆しています。 またSizeに応じた事例数の偏りも大きく、特に100平米を超える/20平米を下回る物件の取引事例は少なくなっています。
以下の各点は、Sizeごとに計算された平均値を図示します。
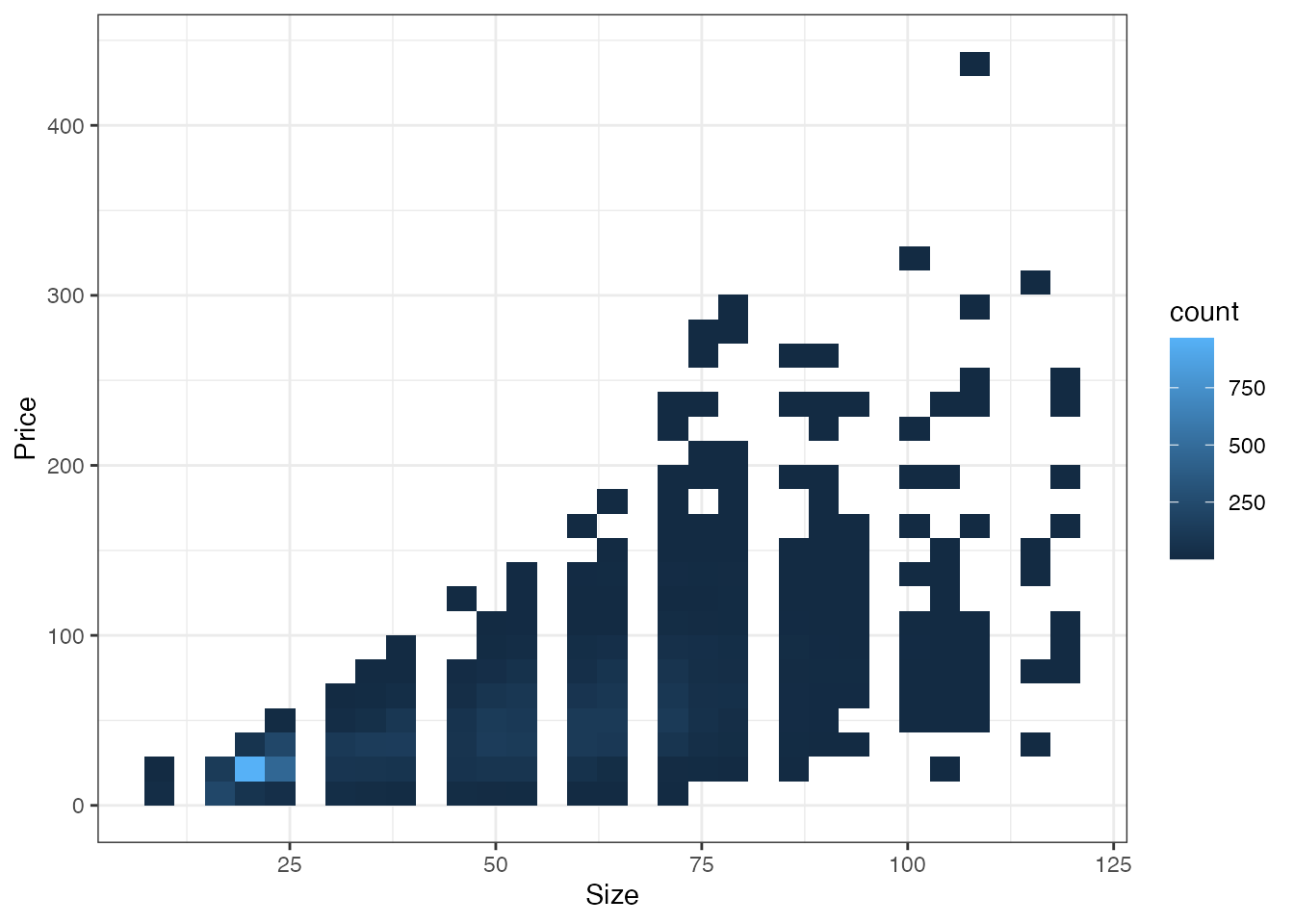
同図からは、 部屋が広くなると平均取引価格は高くなる傾向が読み取れます。
多くの応用で、このような\(X\)ごとに集計するだけでは、現実の社会や市場の特徴について論じることは不適切です。 本ノートでは、以下の少数事例の問題の解決に注力します。
1.3 少数事例の集計
平均値は有力な要約方法ですが、算出に使用する事例の数に注意してください。 部屋の広さ (Size) ごとの事例数は、以下の通りです。
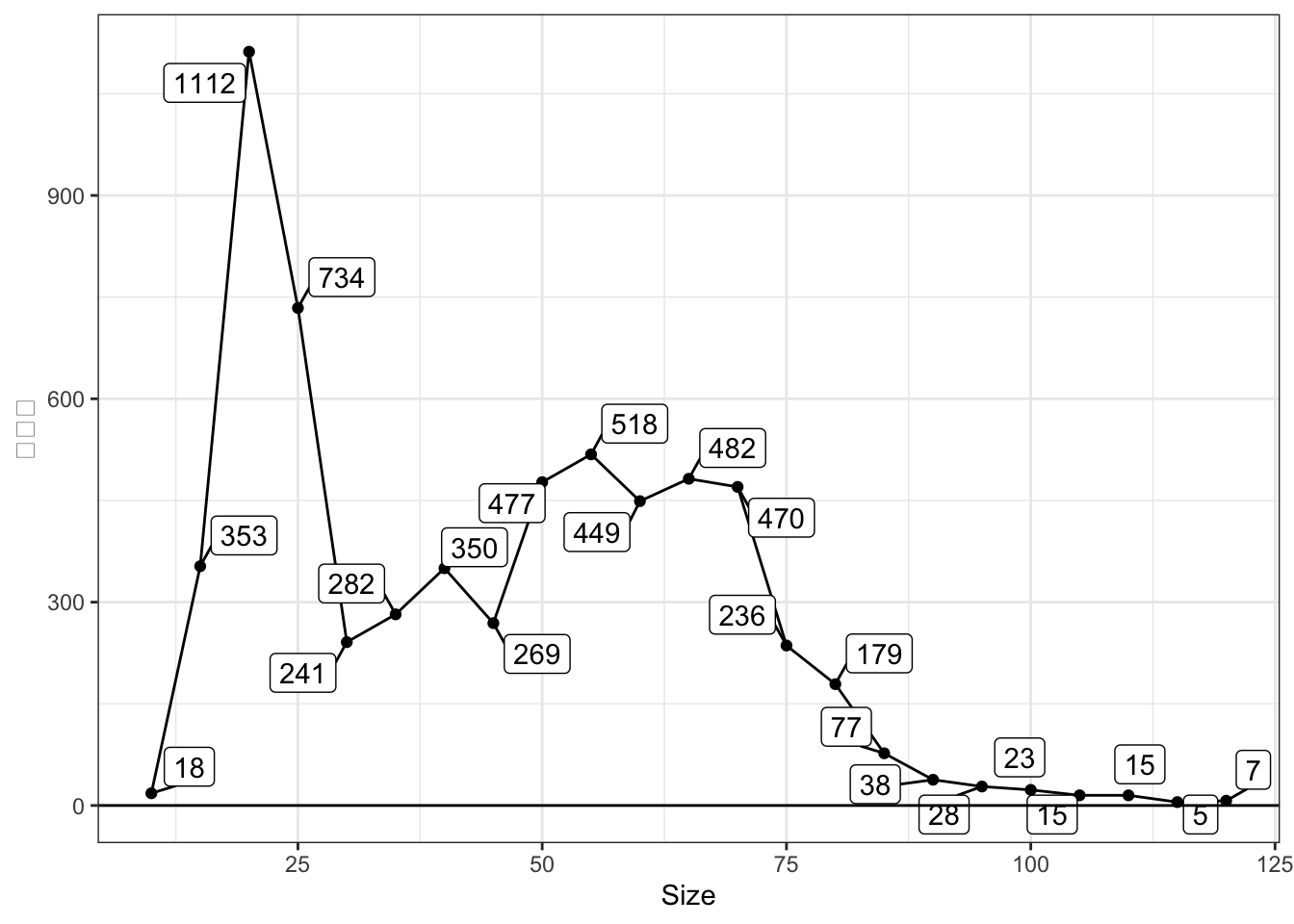
特に20平米を下回る/100平米を超える物件について、事例が少なくなっており、5事例前後の組み合わせも散見されます。 このような小規模な事例数からの計算は、多くの問題が発生します。
以下、Chapter 2 では、事例数が少ないと、平均値も各事例の観察できない変数の偏りの影響を強く受ける可能性を指摘します。 Chapter 3 と Chapter 5 では、このような小規模事例の集計問題を緩和するための手法として、OLSやLASSOを紹介します。