1 バランス後の比較
典型的なバランス後の比較 (Balanced Comparison)分析 では、グループ\(D\)の間で、\(X\)についての差を解消した後に、\(Y\)についての平均差を推定します 1。 このような比較は、格差分析や因果効果の肝となります。
まず実例から紹介します。
1.1 不動産市場の年次比較
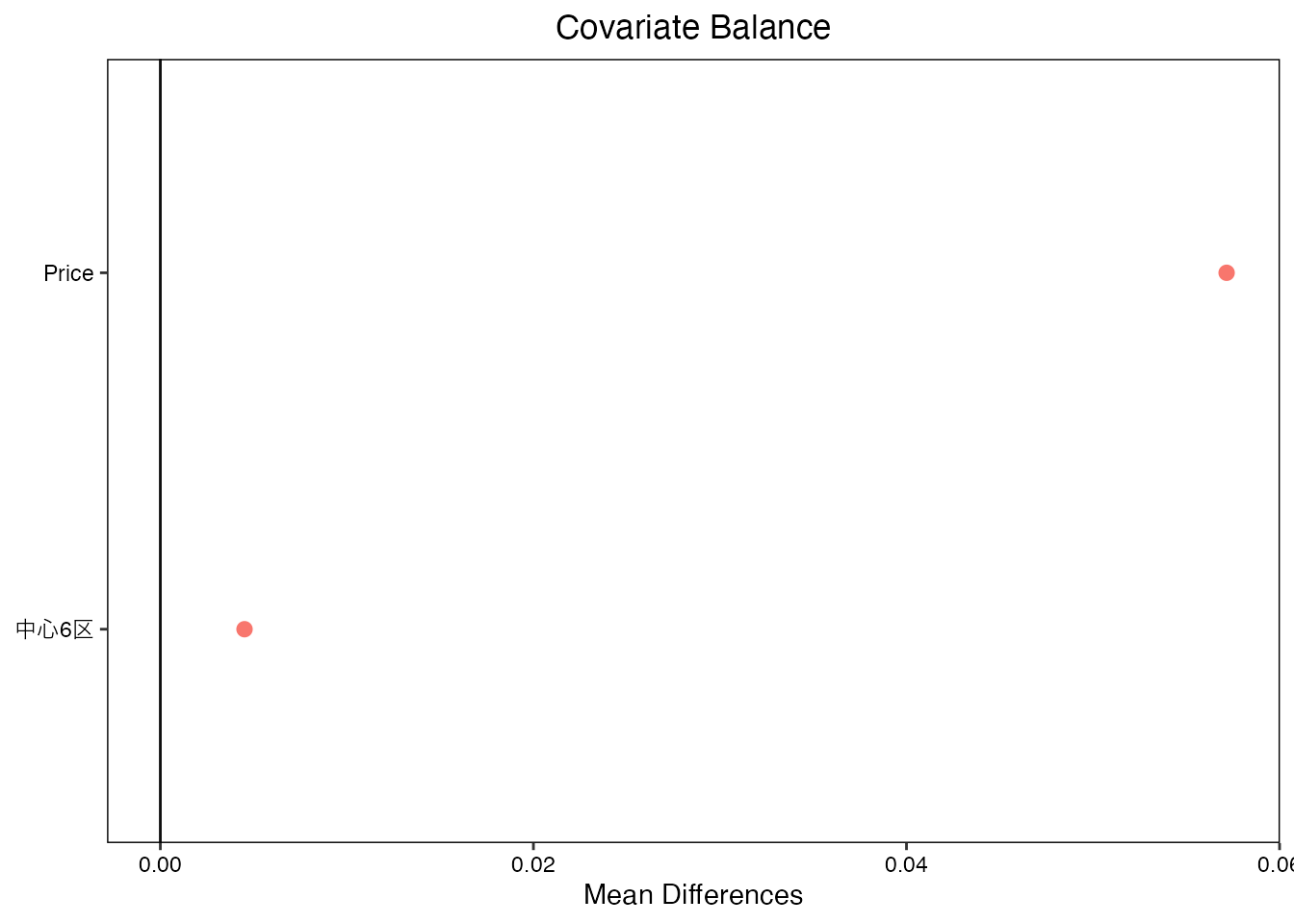
東京23区の中古マンション市場において、2022年と2021年の取引価格と立地(中心6区(港区、中央区、文京区、千代田区、渋谷区、新宿区)、かそれ以外か)について、平均的な差を図示します。
2022年の平均取引価格は、2021年に比べて上昇しており、不動産市場における価格上昇が続いているように見えます。 しかしながら、同時に中心6区の物件割合も増加しています。 一般に中心6区に立地する物件の方が、高い取引価格が予想されます。 このため物件の立地の変化によって、取引価格の上昇が”底上げ”されている可能性があります。
もし中心6区の物件割合が不変であった場合、平均取引価格にどのような差が残るでしょうか? このような問いに対して、バランス後の比較分析は回答できます。
以下では実際のデータを用いて、取引年と立地(中心6区 であれば1、それ以外であれば0)ごとに、平均取引価格を示しています。 また各取引年における取引事例の立地割合も算出しています。
| Example | |||
|---|---|---|---|
| 平均価格(100万円) | 中心6区 | 取引年 | 事例割合 |
| 37.748 | 0 | 2021 | 0.784 |
| 60.474 | 1 | 2021 | 0.216 |
| 39.150 | 0 | 2022 | 0.779 |
| 64.814 | 1 | 2022 | 0.221 |
繰り返し期待値の法則を用いると2022年と2021年の平均取引価格の差を算出できます。
- 変数\(Y,D\)と他の変数\(X\)について、\(Yの平均値\)は以下のように書き換えられる。
\[(D=d)におけるYの平均値\]
\[=(D=d,X=x_1)を満たす事例のYの平均値\] \[\times (D=d,X=x_1)を満たす事例の割合\]
\[+..\]
\[+(D=d,X=x_L)を満たす事例のYの平均値\] \[\times (D=d,X=x_L)を満たす事例の割合\]
- ただし \(X\)がとりえる値は、\(x_1,..,x_L\) とする。
Exampleに適用すると、2022年の平均取引価格は以下のように計算できます。
\[2022年の平均価格\]
\[= \underbrace{64.814}_{中心6区における平均価格}\times\underbrace{0.221}_{中心6区に立地する事例の割合}\] \[+ \underbrace{39.150}_{中心6区以外における平均価格}\times \underbrace{0.779}_{中心6区以外に立地する事例の割合}\]
\[=44.810\]
2021年の平均取引価格も同様に計算できます。
\[2021年の平均価格 = 60.474\times0.216 + 37.748\times 0.784=42.658\]
2022年と2021の平均差を計算すると、2022年の平均取引価格の方が、2.153ほど高くなっていることが確認できます。
繰り返し期待値の法則自体は、シンプルな計算ルールですが、「\(X\)のバランス」の意義を明確にします。 繰り返し期待値の法則から、平均価格の違いは、同じ立地内での平均取引価格の違いと立地の割合の違いによって生じることがわかります。 2021年と比べると、2022年に取引された物件の中で、中心6区の物件割合が21.6 \(\%\) から 22.1 \(\%\) に上昇しています。 一般に中心6区の方が、物件の価格が高い傾向にあります。 このため、中心6区の物件割合の違いが、平均取引価格上昇の一因となっている可能性があります。
バランス後の比較分析では、「取引されている物件に占める中心6区の割合が、変化しなかった場合」の 平均取引価格の変化を推定します。 より一般的には、「\(X\)についての差を解消した状態で」\(D\)間で\(Y\)を比較します。
1.2 バランス後の平均差
本ノートにおいて、バランス後の比較分析の一つである「バランス後の平均差」を推定します。
\[(D=d)におけるYの平均値\]
\[=(D=d,X=x_1)を満たす事例のYの平均値\] \[\times (X=x_1)についてのターゲットとなる割合\]
\[+..\]
\[+(D=d,X=x_L)を満たす事例のYの平均値\] \[\times (X=x_L)についてのターゲットとなる割合\]
- ターゲットとなる割合は、\(D\)の値にかかわらず同じ値として、研究者が定める。
バランス後の平均値の計算例として、以下ではターゲットを取引年にかかわらず、「中心6区が0.25, その他が0.75」と設定し、Exampleに適用します。
| 平均価格 | 中心6区 | 取引年 | 事例割合 | ターゲットとなる割合 |
|---|---|---|---|---|
| 37.748 | 0 | 2021 | 0.784 | 0.750 |
| 60.474 | 1 | 2021 | 0.216 | 0.250 |
| 39.150 | 0 | 2022 | 0.779 | 0.750 |
| 64.814 | 1 | 2022 | 0.221 | 0.250 |
ターゲットのもとでは、取引年にかかわらず、中心6区とそれ以外に立地する事例の割合は一定となります。 このため平均価格の変化を生み出す要因から、事例割合の変化を排除できます。
事例割合をターゲットに差し替えて、繰り返し期待値の法則を適用すると、バランス後の平均価格は以下のように計算できます。
\[2022年のバランス後の平均価格\]
\[= 64.814\times\underbrace{0.25}_{中心6区についてのターゲット}\] \[+ 39.150\times \underbrace{0.75}_{中心6区以外についてのターゲット}=45.566\]
\[2021年のバランス後の平均価格 = 60.474\times0.25 + 37.748\times 0.75=43.4295\]
バランス後の平均差は、2.1365であり、バランス前(2.153)に比べて縮小しました。
1.2.1 Overlapの仮定
バランス後の平均差が計算できる前提条件は、Overlapの仮定 (Positivityの仮定とも呼ばれます) が成り立っていることです。
- ターゲットとなる割合が0よりも大きい\(X\)の組み合わせについて、\(D=1\)の事例も\(D=0\)の事例も、両方存在する: \[1 > \Pr[D=d|X] >0\] ただし \(\Pr[D=d|X]\) は\((X=x)\)内での\(D=d\)の割合(\(D=1\)の割合)
Overlapが成り立っていない場合、全ての\(D\)について平均値が計算できず、厳密なバランス後の比較は根本的に不可能です。
例えば、教育経験\((=X)\)をバランスさせた男女間\((=D)\)での賃金格差を推定したいとします。 もしデータにおける男女間での教育経験の分断が極めて大きい場合、大学卒以上の女性は存在しない可能性があります。 この場合、\(X=大学卒\)の女性割合は\(0\)であり、大学卒内で男女間比較は不可能です。 このため大学卒について、ターゲットとなる割合を”0”としない限り、バランス後の比較は不可能です。
1.3 応用事例
バランス後の比較分析の応用例は、大量に存在します。 以下では実務においてよく利用されている指標を紹介します。
1.3.1 既存店ベースの比較
バランス後の比較は、企業の経営戦略を考える上でも用いられます。
小売や飲食/宿泊業などでは、しばしば既存店に絞った上での、売上比較がなされます。 例えば、あるコンビニチェーンで、店舗あたりの平均売り上げが1000万円増大したとします。 同時に去年から今年にかけて、新規出店も大きく増加したとします。 新規店の方が売上が高くなる傾向がある場合、新規店割合の違いが、平均売上の上昇をもたらした可能性があります。
既存店割合をバランスさせるシンプルな方法として、既存店のみに絞った平均売上を比較がよく行われます。 このような分析では、既存店比率は全ての年について\(100 \%\)となり、完全なバランスが達成されます。
既存店ベースの比較におけるターゲット割合は、新規店については1、新規店以外については0となります。
1.3.2 合計特殊出生率の時点/地域間比較
バランス後の比較分析は、社会/政策分析においても幅広く利用されています。 代表例は、合計特殊出生率の国家間/時代間比較です。
出生数の動向を把握する上で、新生児数を年次や国家間比較は、有益だとみなされてきました。 合計特殊出生率 は、成人の年齢構造の違いをバランスさせるために利用されている指標です。 単純な出生率(一年間に生まれた子供の数/女性の数)は、成人の年齢構造の影響を強く受ける可能性があります。 社会において高齢者の比率が高まれば、出生率は低下することが予想されるからです。 対して合計特殊出生率は、「仮に年齢構造が同じであった場合」の出生率を、以下の方法で推定しています \[\frac{15歳の女性が産んだ子供の数}{15歳の女性の数} +..+ \frac{49歳の女性が産んだ子供の数}{49歳の女性の数}\]
合計特殊出生率の計算においては、15歳から49歳の女性の年齢 (\(=X\))層が同じ割合になることを目指しています。 すなわちターゲット割合は、15歳から49歳までについて 1/34、それ以外の層については”0”となります。
1.3.3 物価指数
より複雑な比較が要求される指標の代表例は、物価指数です。 物価指数は、“同じような消費生活”を送るために必要な支出額を、比較するために算出されます (wiki)。 この際に問題となるのは、実際に消費する商品の組み合わせや量は、年毎に変化することです。 すなわち \(D=\) 時点、\(Y=\) 名目価格、\(X=\) “品目”とし、消費する”品目”をバランスさせる必要があります。
Bajari et al. (2023) は、機械学習の手法と商品の画像やテキストデータも用いることで、”質”も含めてバランスする試みを行なっています。 このような分析によって、“ステレス値上げ”や”商品の質的改善”にも対応できる指標が作成できる可能性があります。
1.3.4 因果効果
バランス後の比較は、因果効果を推定する際にも、中心的な役割を果たします。 因果効果を記述する枠組みは、多数提案されています (Pontial outcome/Structural Equation Model (DAG)/ 経済モデルなど)。 これらは共通して、思考実験、(特に反実仮想実験)の重要性を指摘しています。
ここでは反実仮想を明らかにできる仮想的な実験 (Target trial) を想像します。 典型的には、「無限大の被験者を用意し、被験者間の相互作用がない環境で、ランダムに選ばれた一部の被験者に介入を行う」実験です。 このような実験結果をもし得ることができれば、介入を行った/行わなかった被験者を比較することで、介入の因果効果を明らかにできます。 介入は完全ランダムに決まっているため、介入を行った/行わなかった集団間で、背景属性について大きな差が生じないことを担保できます2。
現実に、このような大規模な実験を行うことは不可能です。 このため現実のデータから、理想的な実験結果を可能な限り再現することを目指します。
Egami et al. (2024) は、TVゲームが精神的健康状態に与える因果効果について、実証的な証拠を提供しています。 同論文では、コロナ下で生じたゲーム機への過大需要と、それに対応するために実施された「ゲーム機購入権くじ」を利用しています。 同時期においては、ゲーム機購入希望者の中で、くじに当選した人だけゲームを購入することができました。 このため理想的な実験に近い状況が生じています。
しかしながら、理想的な実験とは異なり、背景属性に幾つかの違いが生じる可能性があります。 例えば地域によってくじの当選確率が異なるのであれば、ゲーム機購入者と非購入者の間で、居住地に偏りが生じてしまいます。
以上に対応するために、\(D=\) くじに当選、\(Y=\) 健康状態、 \(X=\) 居住地等とし、当選/非当選者間で背景属性をバランスさせた推定を行なっています。
1.3.5 格差分析
格差分析においても、バランス後の比較は重要です。 格差分析の出発点は、通常格差/差別/不平等の大きさの推定です。 このためには、研究対象とする格差を明確に定義する必要があります。
因果効果と同様に、格差の定義についても、多様な議論があります (ヒュームの法則; Jackson and VanderWeele (2018); Rose (2023); Mossé et al. (2025) )。 代表的なものとして、格差や差別を因果的に定義するのは難しく、あくまで規範的に定義する立場があります。 すなわち「本来であれば存在すべきではない差」を格差として定義します。
例えば、両親の教育経験間での、子供の所得格差に関心があるとします。 両親の属性に基づく差は、機会の不平等の代表的な例であり、多くの研究が行われてきました。
実証上の論点は、両親の教育経験が異なれば、子供の年齢の分布も異なる可能性への対処です。 日本のような教育年数が急激に伸びた国においては、教育年数の長い両親の子供は、年齢が若い可能性があります。 また年功的賃金体系が残存していることを踏まえれば、年齢が若ければ賃金が低い傾向があります。 このため単純比較を行い、「教育年数の長い両親の子供の方が、短い両親の子供よりも所得が低い」、という結果を得たとしても、この差は年齢分布の違いを反映している可能性があります。
もし研究関心が、「同じ世代なのに両親の教育経験によって生じる格差」にあるのであれば、子供の生まれ年を\(X\)としてバランスする必要があります。
またバランスは格差の要因分析にも応用できます。 このような分析は、分解分析 (Decomposition analysis)と呼ばれます (Opacic, Wei, and Zhou 2025)。 Vafa, Athey, and Blei (2024) では、男女間賃金格差の要因分析として、\(X=\) 職歴、\(D=\) 性別、\(Y=\) 賃金、とするバランス後の比較を行なっています。 職歴のバランス後にも、賃金格差が残存しているのであれば、採用時や個別賃金交渉における男女間での異なる取り扱いが男女間格差の要因であると解釈できます。
1.4 応用上の課題
バランス後の比較は、シンプルな枠組みです。 上記の例の通り、大規模なデータを用いて、少ない\(X\)をバランスさせるのであれば、単純な計算でバランスできます。
しかしながら、多くの応用では複数の\(X\)を同時にバランスさせることが求められます。 このような応用では、同じ属性を持つ事例数が少なくなり、実際の計算は困難になります。
多くの応用で活用できる、より実践的な推定方法が求められます。 このような推定手法は、Balancing Weight (Chapter 3) を実質的に推定していると解釈できます。 Chapter 2 ではBalancing Weightを理解するための準備として、一般的なWeightを紹介します。