4  OLSによる特徴のバランス

\(X\) の組み合わせが多く、Balancing weightsを計算することが困難な場合、近似的なバランスが有力な方法となります。

本節では代表的な統計手法であるOLS（重回帰）が、近似的なBalancing weightsを暗黙のうちに計算する手法であることを紹介します。 OLSは分布の特徴を、研究者が定める定式化に応じて、要求するBalanceの精度を変更できることが利点です。 ただし、\(D\) 間での\(X\)の分布の分断が激しい場合、予期せぬ挙動を示しやすいことに注意が必要です。

4.1 OLSによる平均値のバランス

近年の研究により、線型モデルのOLS推定は、近似的な Balanceを達成することが確認されています (Chattopadhyay and Zubizarreta 2023)。 本ノートでは、\(D=\{0,1\}\)を前提とし、その議論の骨子を紹介します。

OLSの性質 (Chattopadhyay and Zubizarreta 2023)

• \(Y\sim D + X_1 + .. + X_L\) をOLSで推定し算出される \(D\) の係数値は、以下の方法で計算される値と完全に一致する

1. すべての\(X_l\) について、以下を満たす \(\omega(x,d)\) を探す。

\[(D=1)における(\omega(x,1)\times X_l)の平均値\]

\[=(D=0)における(\omega(x,0)\times X_l)の平均値\]

2. 1.を満たす\(\omega(x,d)\) の中で、最小の分散を持つ \(\omega(x,d)\) をBalancing Weightsとする

3. \(\beta_D\) を以下のように計算する。 \[\beta_D=(D=1)における(\omega(x,1)\times Y)の平均値\]

\[-(D=0)における(\omega(x,0)\times Y)の平均値\]

重回帰による推定は、\(D\)間で\(X\) の平均値をバランスさせた上で、平均値を比較しています。 また「母集団におけるOLSの結果」の推論に悪影響を与える、Weightの分散も可能な限り削減しています。

4.1.1 例

部屋の広さ (Size) と 築年数 (Tenure) をバランスさせた後に、2022(\(D=1\))/2021(\(D=0\))年の平均取引価格差を推定します。 \(Price\sim D + Size + Tenure\) をOLSで推定したとします。

estimatr::lm_robust(
  Price ~ D + Size + Tenure, 
  Data)

この推定によって得られる \(D\) の係数値は、以下のようなバランスを達成するBalancing Weightsを用いた平均差と一致します。

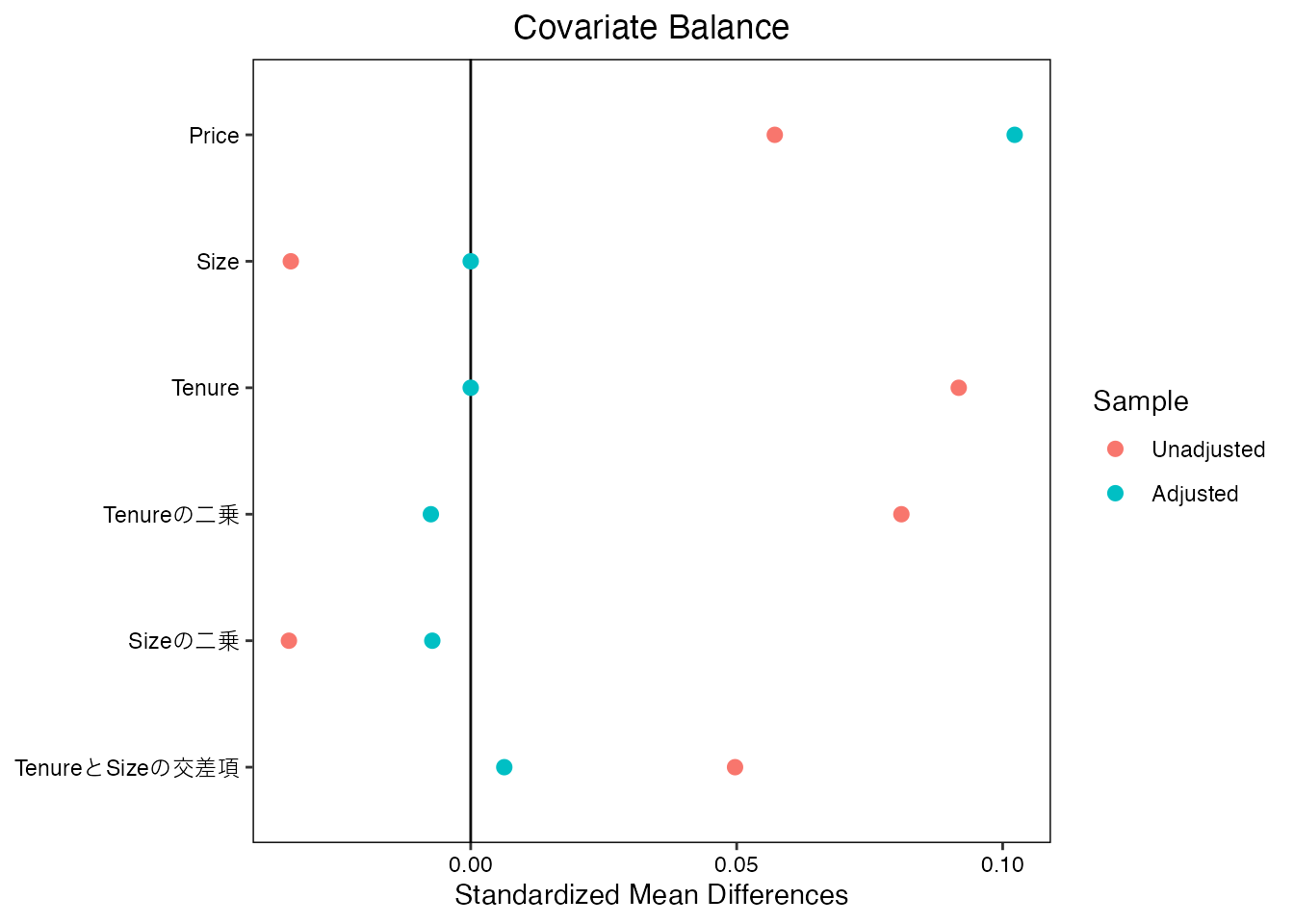
赤点 (Unadjusted) は、バランス前の単純平均差を表します。 価格が大きく上昇していますが、取引物件の部屋の広さは狭くなり、築年数は古くなっています。 青点 (Adjusted)は、OLSによる暗黙のバランス後の差を示しています。 SizeやTenureの平均値は完全にバランスしており、結果平均取引価格差も上昇しています。 Tenure2やSize2は、築年数や部屋の広さの二乗項(分散)、Tenure_Sizeは交差項(共分散)を示しており、これらについてはバランスしていません。

4.2 OLSによる分散や共分散のバランス

\(Price\sim D + Size + Tenure\) を推定しても、SizeやTenureの平均値のみしかバランスできません。 一見、これはOLSの致命的な弱点のように見えますが、簡単な修正によって解決できます

分散や共分散もバランスさせるためには、二乗項や交差項もモデルに導入したモデル \[Price\sim D + Size + Tenure + Size^2 + Tenure^2 + Tenure\times Size\] をOLS推定します。

estimatr::lm_robust(
  Price ~ D + Size + Tenure +
    I(Size^2) + I(Tenure^2) +
    (Size + Tenure)**2, 
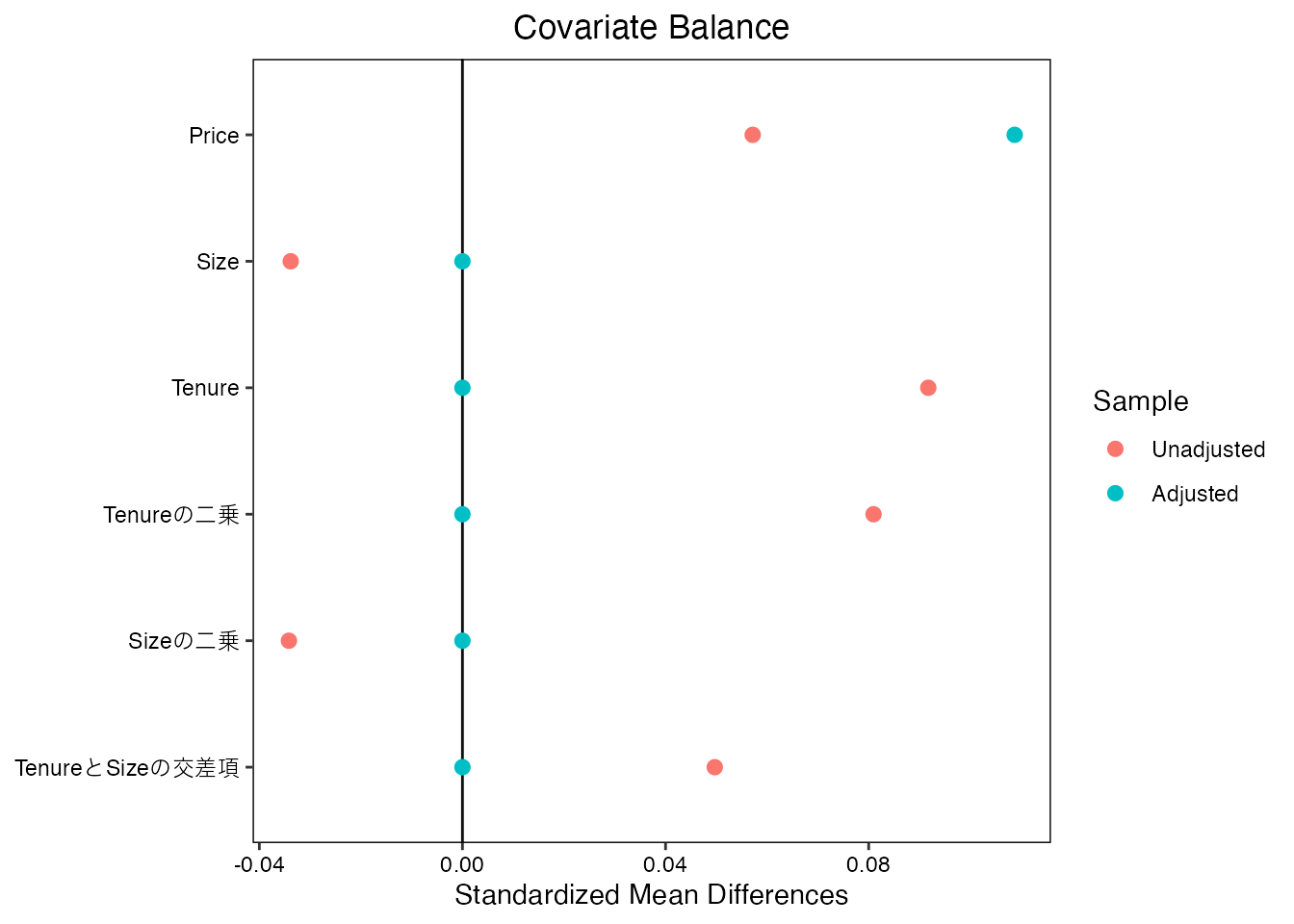
  Data)

これによって、Sizeの二乗の”平均値”などもバランスさせることができます。 これは各変数の分散や共分散をバランスを意味します。 結果、以下の図の通り、分散や共分散もBalanceします。

4.3 母集団の推定方法

推定するパラメタ (\(\beta_0,..,\beta_L\)) に比べて事例数が十分に大きければ、データ上のOLSの結果は、「母集団におけるOLSの結果」の優れた推定値です¹。 特に近似的に計算される信頼区間を用いれば、母集団におけるOLSの結果を、定量的に議論できます。

以下では一切の\(X\)をバランスさせないケース、SizeとTenureの平均値のみをバランスさせるケース、平均に加えて分散と共分散もバランスさせたケースの推定結果を、\(95\%\) 信頼区間とともに比較しています。

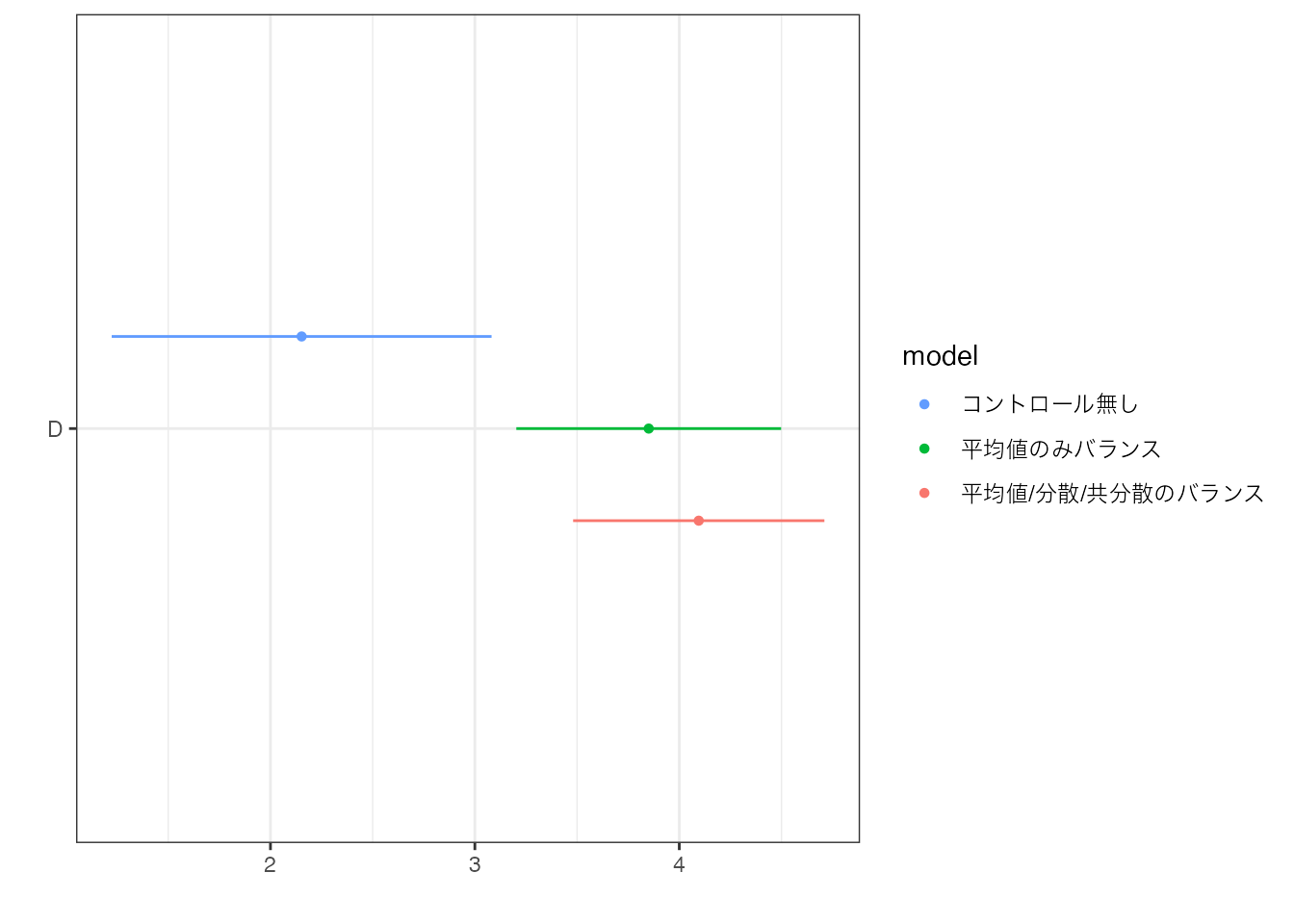
コントロールをしないケースに比べて、SizeやTenureをバランスさせると、2022年と2021年の平均差が大きくなりました。 一方で本データについては、平均値に加えて分散や共分散をバランスさせたとしても、あまり大きな変化は生じませんでした。

また信頼区間に焦点を当てるとバランス後の平均差の方は、前に比べて、より「狭く」なっています。 これは、母集団におけるOLSの結果とデータ上のOLSの結果が、大きく乖離する可能性が減少している (と推測できる) ことを反映しています。

4.4 実践への示唆

実践における課題は、\(X\) について適切な複雑さを持つモデルを設定することです。 しかしながら適切な複雑性は、母集団の特徴や事例数などに依存しており、一般 な解決は困難です。 ただし過去の実践の問題点、および実践上の示唆を得ることはできます。

多くの研究で\(X\)の二乗項や交差項を導入しない推定が行われてきました。 しかしながらこのような推定は、平均値のみのバランスにとどまり、不十分な可能性が高いと考えられます。 例えば、NBER Summer Institute 2018における、Esther Dufloのチュートリアル では、連続変数については二乗項、および全変数について交差項を導入した推定を行なっています。

複雑な推定は、母集団における推定結果の推論を困難にします。 この問題は、事例数が少ない小規模データを用いた推定において深刻です。 しかしながら現代的な分析環境のもとでは、1000事例を超えるデータを用いた推定が一般的になっています。 このため、バランスさせたい\(X\)の数が少ない場合、その二乗項や交差項を加えたとしても、悪影響は小さいと考えられます。 少なくとも小規模事例を用いた推定よりも、より複雑なモデルを推定すべきであると考えられます。

バランスさせたい変数 \(X\) の数が多い場合、二乗項や交差項を導入するとモデルが爆発的に複雑化し、OLSでは推定できなくなります。 このような場合は、Chapter 6 で議論する通り、機械学習を応用が有力です。

4.5 実践上の課題

OLSにより暗黙のうちに計算されるWeightは、平均値をバランスします。 しかしながら、Balancing weightsに求められる他の性質は必ずしも満たされません。 以下、OLSの抱える問題点を列挙します。

以降の章で紹介する手法の利点は、このOLSが抱える問題点を改善することにあります。 このため発展的な手法を理解し、活用するためにも、OLSの問題点をしっかり認識する必要があります。

4.5.1 定式化

OLSにおいては、分布の特徴をどこまでバランスさせるのかが問題となります。 事例数が十分あれば、3乗項などの多くの特徴をバランスさせることが可能です。 しかしながら事例数が少ない場合、大量のモーメントをバランスさせると、推定誤差が大きくなってしまいます。 このため事例数に応じて、バランスの対象とする特徴の数を選択する必要があります。 しかしながら実際の応用において、このような選択を適切に行うことは困難です。

この問題に対して、Chapter 6 では機械学習を用いた改善方法を紹介します。

4.5.2 ターゲット割合

バランス後の\(X\) の平均値がどのような水準になるのか、一般に不透明です。 結果を解釈するためには、\(X\) の平均値は明確な水準、例えばデータ全体での平均値と一致させることが望まれます。 しかしながら、OLSはそのような水準との一致を保証しません。

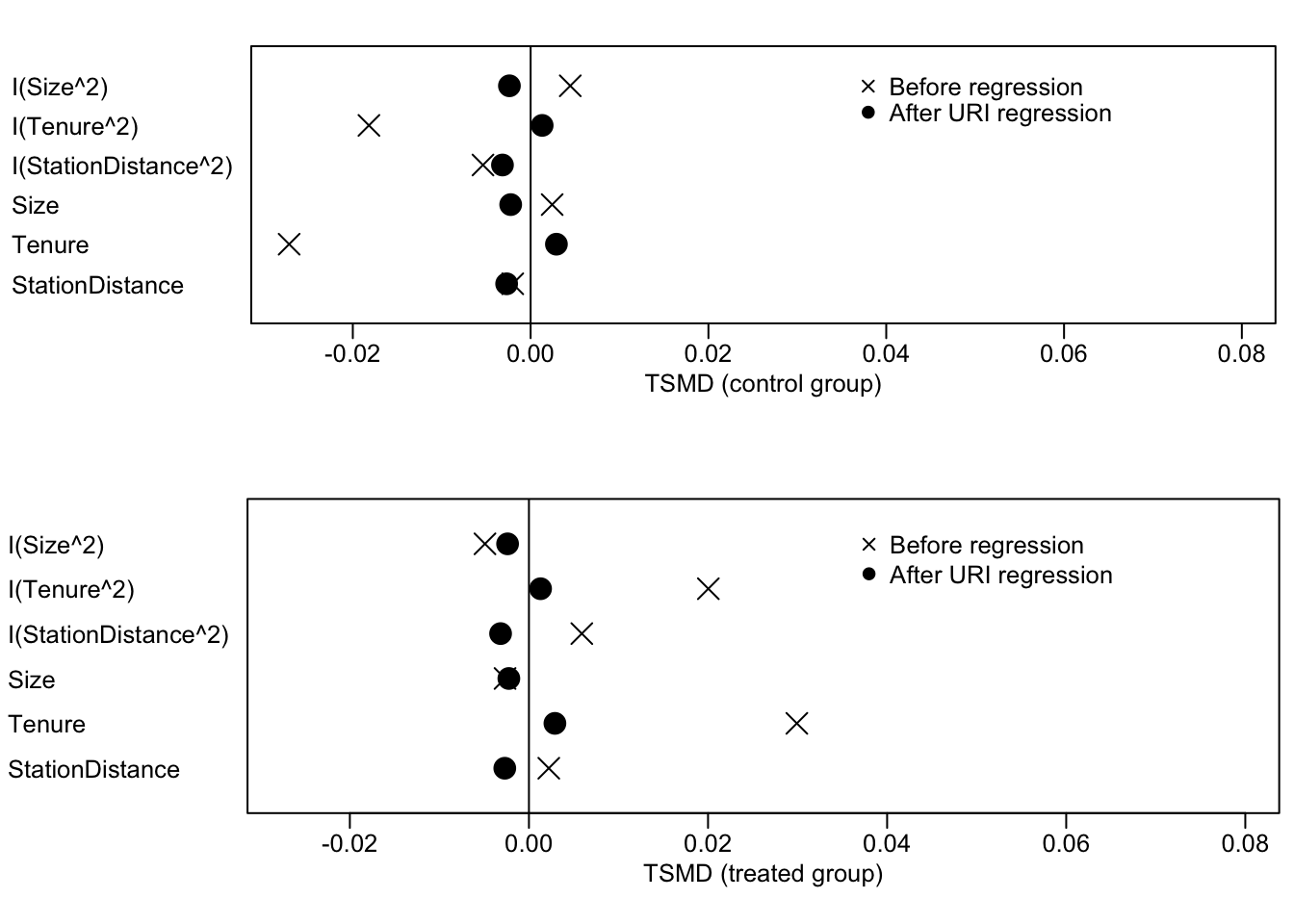
OLSによるバランス後の\(X\)の平均値について、lmw packageにより診断できます。

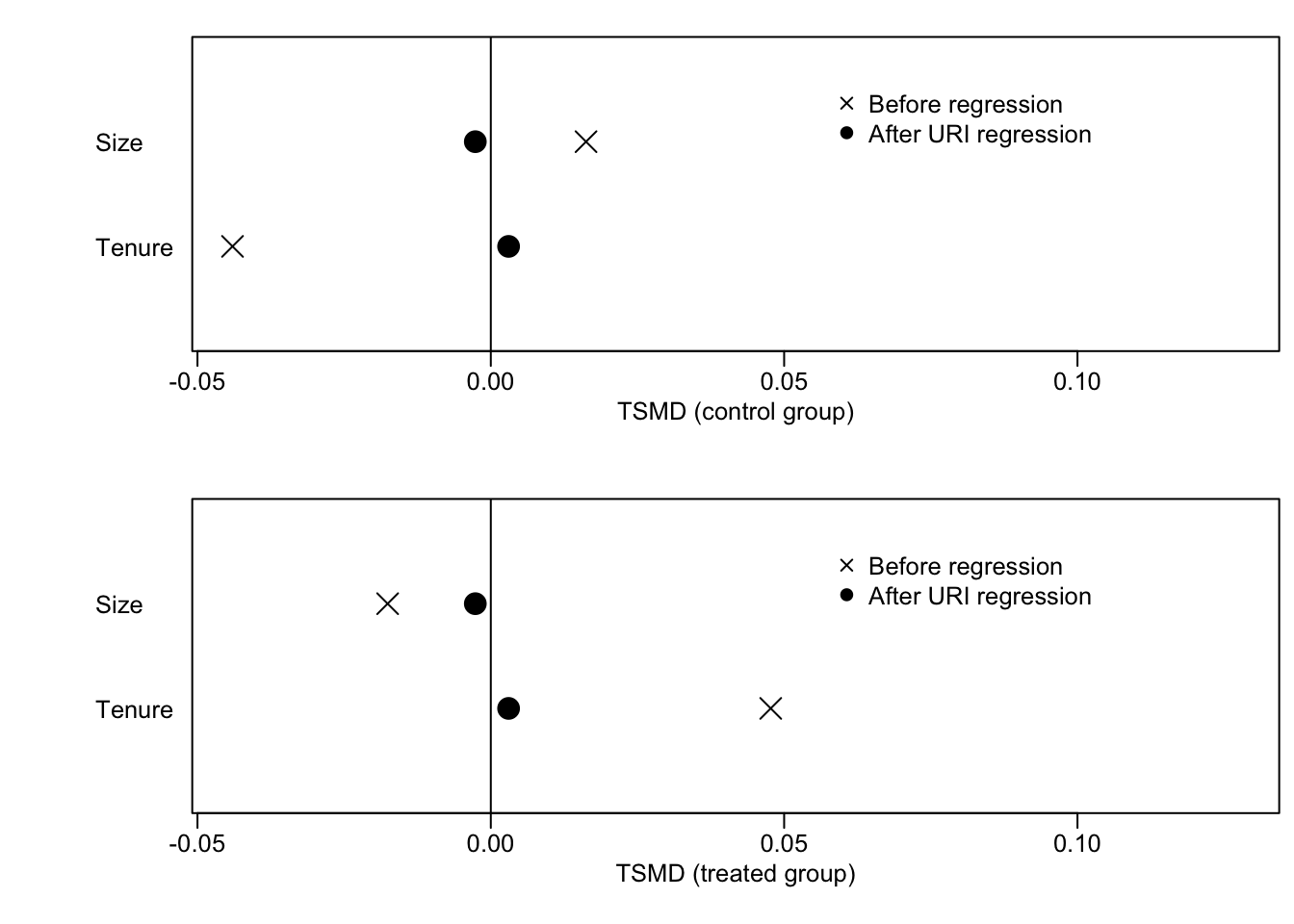
黒丸はOLSによるバランス後、ばつ印はバランス前の平均値を示しています。 Control groupは、\(D=0\) (2021年)、Treatment groupは、\(D=1\) (2022年)の値です。 0線は、サンプル平均を示しています。

同図からバランス前は、2022年についてはSizeがサンプル平均よりも小さく、Tenureは長くなっています。 黒丸を見るとOLSによるバランス後は、2022年と2021年の間で平均差がなくなることが確認できます。 ただし０線からは乖離しており、サンプル平均とは一致していないことが確認できます。

この問題の解決としては、サンプル平均にバランスさせることを明示的に要求したBalancing Weightの算出 (Chapter 5) が有力です。

4.5.3 負のウェイト

Balancing weightsは、正の値を取ることが望まれます。 しかしながらOLSが生成するWeightは、負の値を取る可能性があり、ミスリードな推定結果をもたらす可能性があります。

lmw packageは、OLSが生成するweightsの値を計算します。 例えばhist関数により、ヒストグラムとして可視化できます。

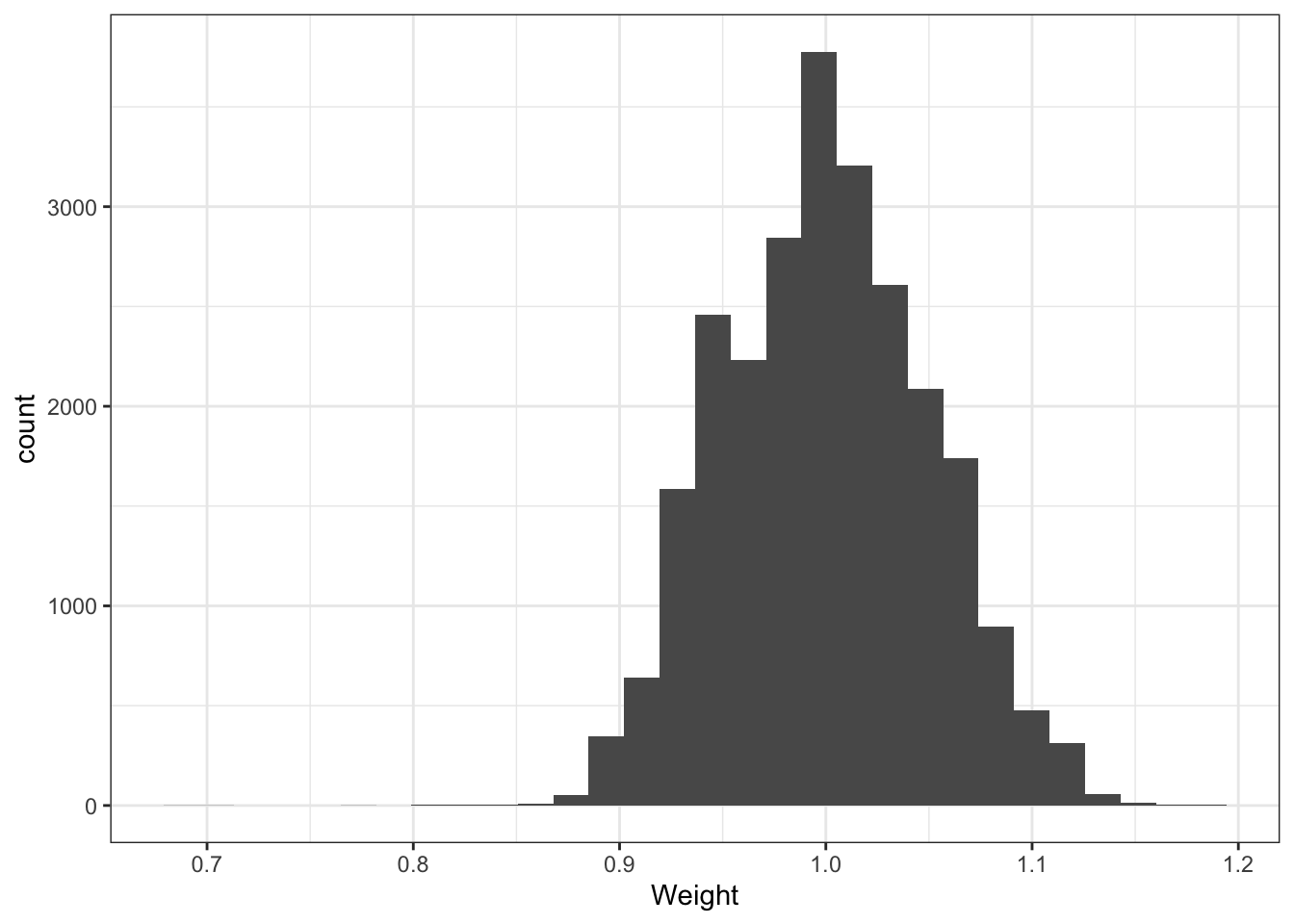
本応用例では、負のweightsは発生していないことが確認できました。

負のweightsが発生しない方法としては、明示的なBalancing Weightの算出 (Chapter 5) や機械学習を活用した柔軟な推定 (Chapter 6)が有力です。

4.6 Rによる実践例

• \(D\)と\(X\)の交差項を含めたモデルのOLS推定、およびその性質の診断は、以下のパッケージを用いて実装できます。

  • readr (tidyverseに同梱): データの読み込み

  • lmw: OLSが計算するbalance weightsを計算

    • Repository

  • estimatr: OLSをRobust standard errorとともに計算

    • Repository

  • dotwhisker: 信頼区間の可視化

    • Repository

4.6.1 準備

データを取得します。 \(D\) として、取引年が2022か2021かで、1/0となる変数を定義します。 シンプルな比較分析について信頼区間は、データ分割は不要です。

Data = readr::read_csv("Public.csv") # データ読み込み

Data = dplyr::mutate(
  Data,
  D = dplyr::if_else(
    TradeYear == 2022,1,0
  ) # 2022年に取引されれば1、2021年に取引されていれば0
)

4.6.2 OLSによるバランス

\(D\) 間でSize,Tenure,StationDistanceの平均値をバランスさせ、Priceの平均値を比較します。 また比較のために、一才のバランスを行わない比較結果も併記します。

Model_NoBalance = estimatr::lm_robust(
  Price ~ D,
  Data) # OLS推定

Model = estimatr::lm_robust(
  Price ~ D + Size + Tenure + StationDistance,
  Data) # OLS推定

dotwhisker::dwplot(
  list(バランスなし = Model_NoBalance, 平均値のみ = Model),
  vars_order = "D") + # 信頼区間の可視化
  ggplot2::theme_bw() # 背景を白地化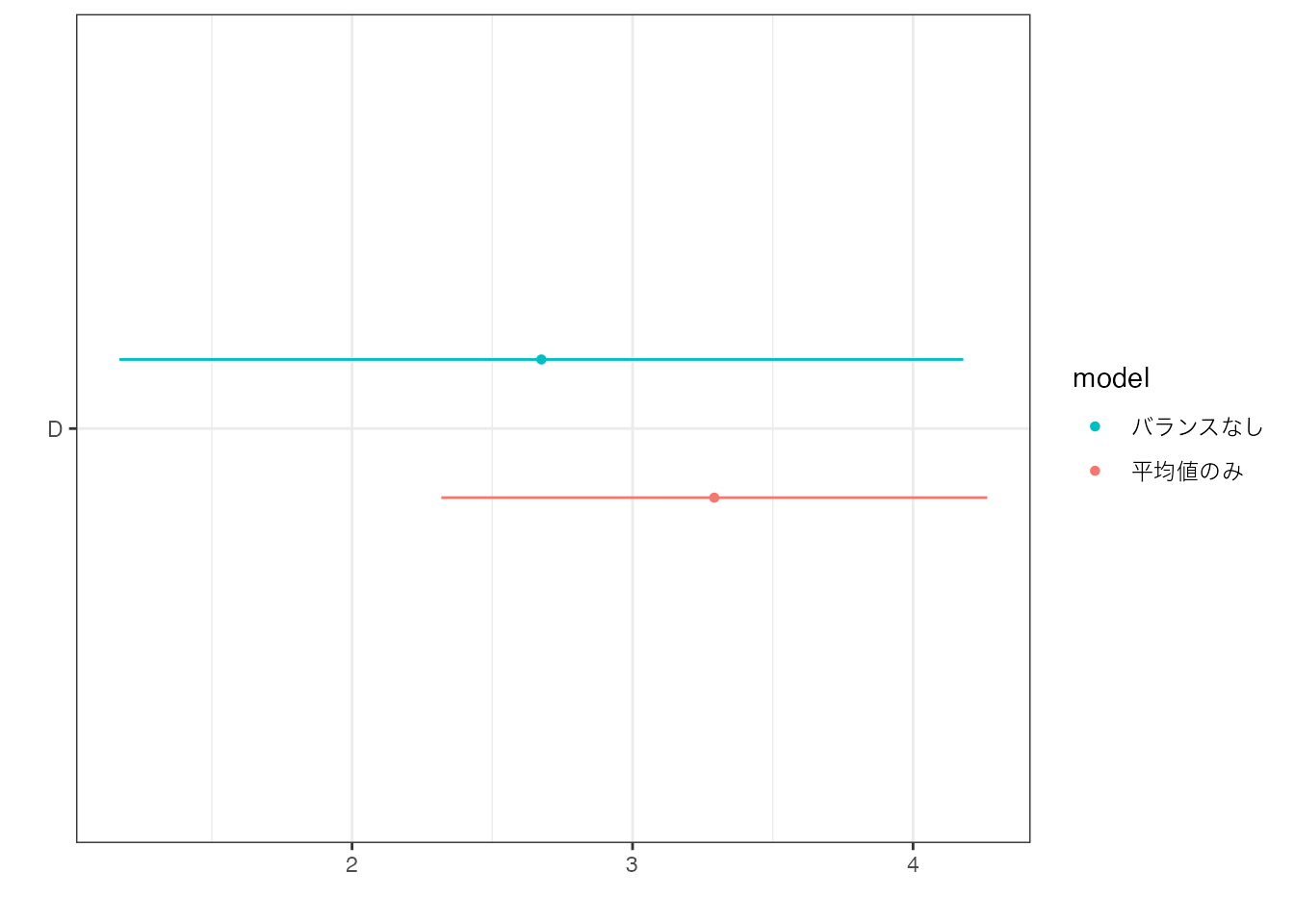

\(D\) の係数値は3.29であり、バランス後も中心6区の物件の方が平均取引価格が高いことがわかります。 また信頼区間を考慮することで、母集団においても、中心6区の物件の方が平均取引価格が高い傾向があることがわかります。

次に各変数の分散と共分散もバランスさせます

ModelLong = estimatr::lm_robust(
  Price ~ D + 
    (Size + Tenure + StationDistance)**2 + # 交差項の作成
    I(Size^2) + I(Tenure^2) + I(StationDistance^2), # 分散
  Data)

バランスをしない単純比較も含めて、推定結果を比較すると以下のようになります。

dotwhisker::dwplot(
  list(
    バランスなし = Model_NoBalance,
    平均のみ = Model,
    `平均/分散/共分散` = ModelLong
    ),
  vars_order = "D"
  ) +
  ggplot2::theme_bw()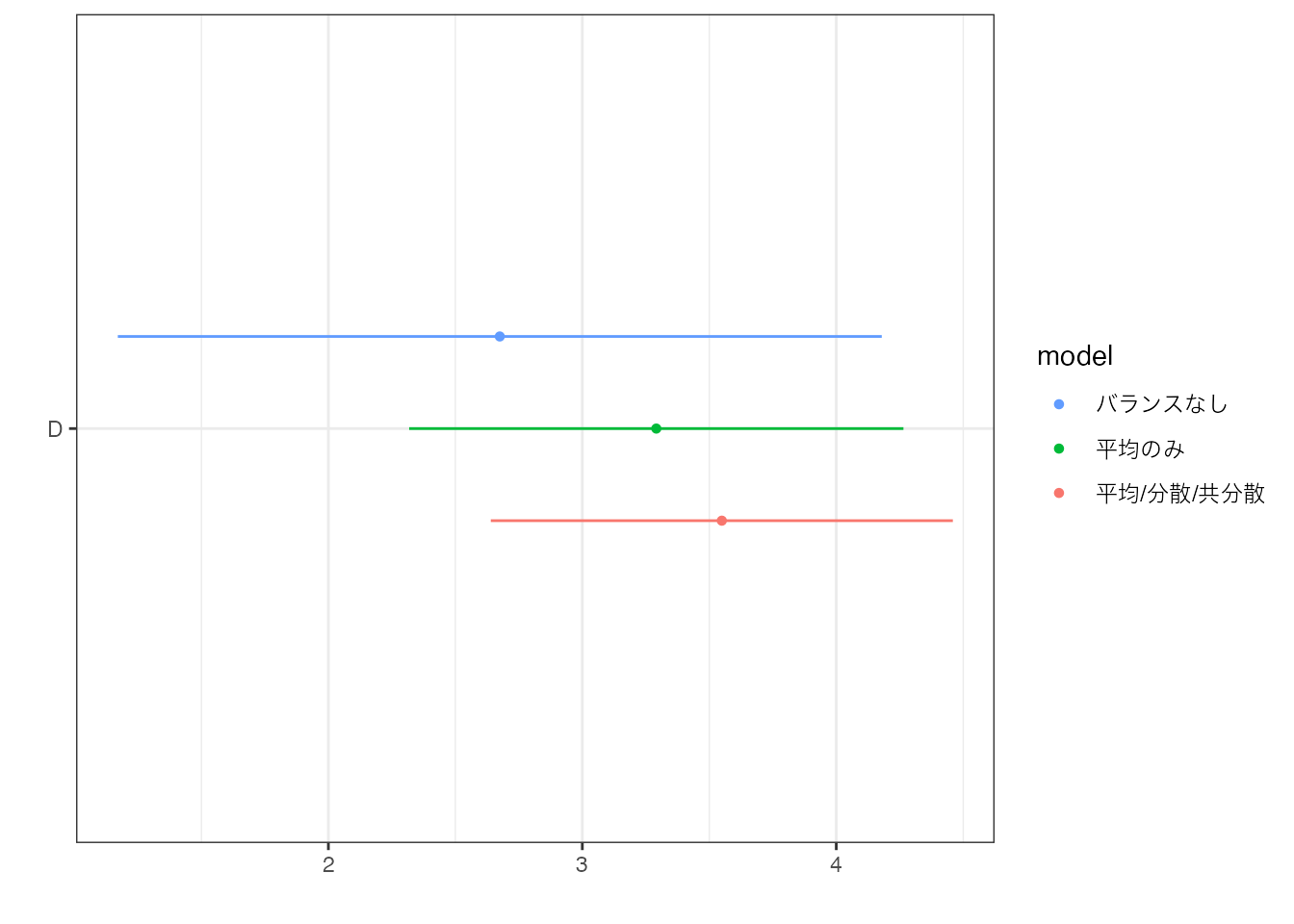

バランスすることで、推定値が大きくなり、信頼区間が縮小する(推定精度が改善する)ことが確認できます。

4.6.2.1 Balanced Weight

lmw パッケージのlmw関数を用いれば、OLSが算出しているBalance weightsを計算できます。

Match = lmw::lmw(
  ~ D + I(Size^2) + I(Tenure^2) + I(StationDistance^2) +
               (Size + Tenure + StationDistance)**2, # 平均、分散、共分散をバランス
  Data
) # Weightの算出

summary(Match$weights) # Weightの記述統計量を図示

   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
 0.7005  0.9685  1.0014  1.0000  1.0335  1.3118 

負のWeightが発生していないことが確認できます。

データ全体での平均値との乖離も、以下のとおり確認できます。

plot(summary(Match), abs = FALSE)

Chattopadhyay, Ambarish, and José R Zubizarreta. 2023. “On the Implied Weights of Linear Regression for Causal Inference.” Biometrika 110 (3): 615–29.

Chernozhukov, Victor, Christian Hansen, Nathan Kallus, Martin Spindler, and Vasilis Syrgkanis. 2024. “Applied Causal Inference Powered by ML and AI.” arXiv Preprint arXiv:2403.02467.

---

1. 詳細に関心がある読者は、Chernozhukov et al. (2024) の１章などを参照ください。