Chapter 7 Regression-discontinuity

  • Regression discontinuityに基づく推定方法を紹介

  • Chapter 7.1 : Regression discontinuityにおける問題意識を紹介

  • Chapter 7.3 : Sharp designに基づく推定方法を紹介

7.1 問題意識

  • 識別の仮定：ある変数\(X\)について、以下の条件を満たすcutoff \(c\)が存在する

    • \(\lim_{x\uparrow c}\Pr[D_i=d|X=x]\neq \lim_{x\downarrow c}\Pr[D_i=d|X=x]\): 原因変数の分布がcutoffの前後で非連続的に変化している

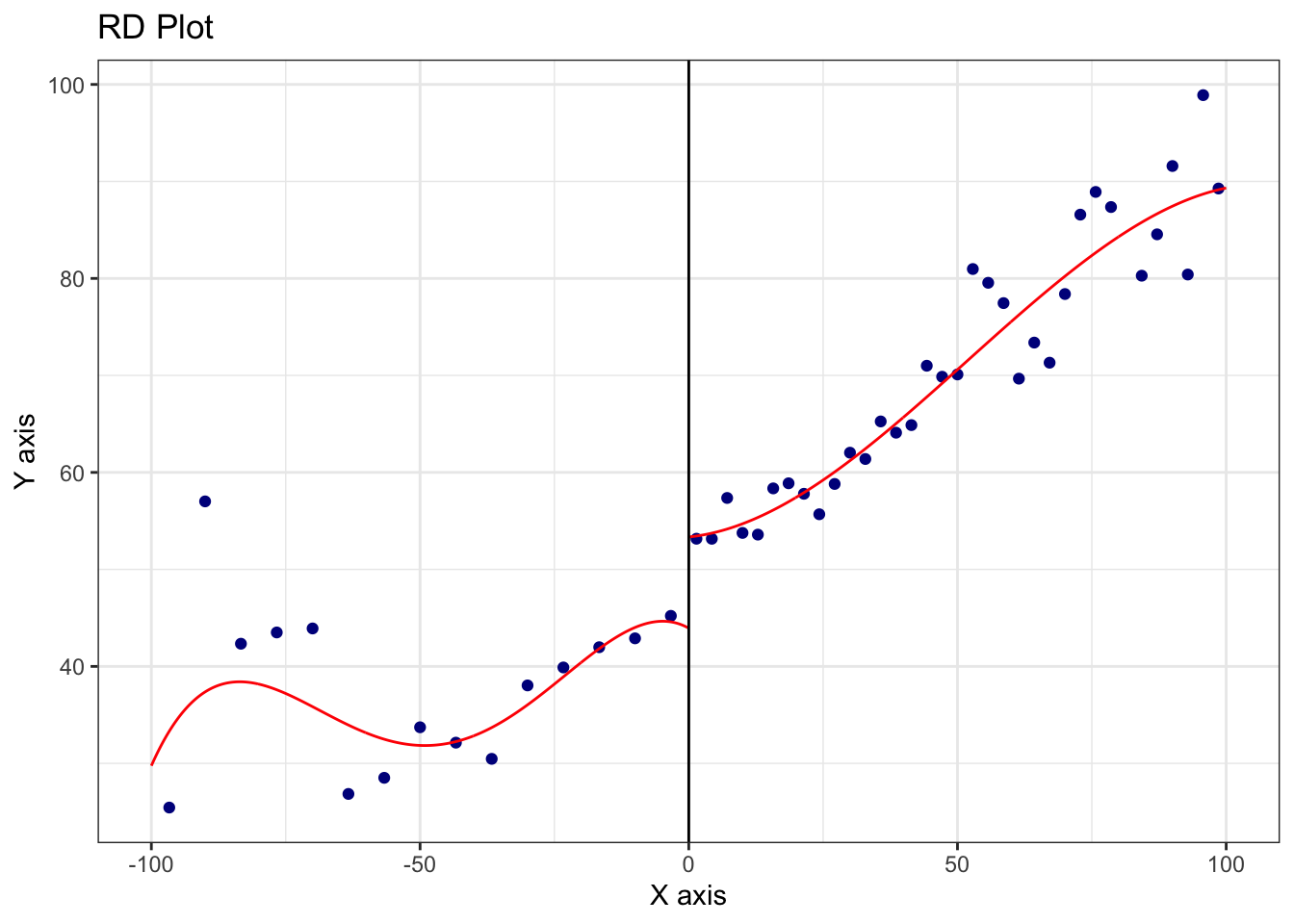
  • 通常、Cutoffの近傍には少数のサンプルしかないので、外挿する必要がある。

  • Local polynomial regressionによる局所的外挿は、rdrobustパッケージ (Calonico et al. 2021)により実装できる。

  • 同パッケージによる実装も含んだ包括的な入門は Cattaneo, Idrobo, and Titiunik (2019b), Cattaneo, Idrobo, and Titiunik (2019a).

7.2 パッケージ & データ

  • Rdrobustに同梱されれいるExample data (Cattaneo, Frandsen, and Titiunik 2015)を使用

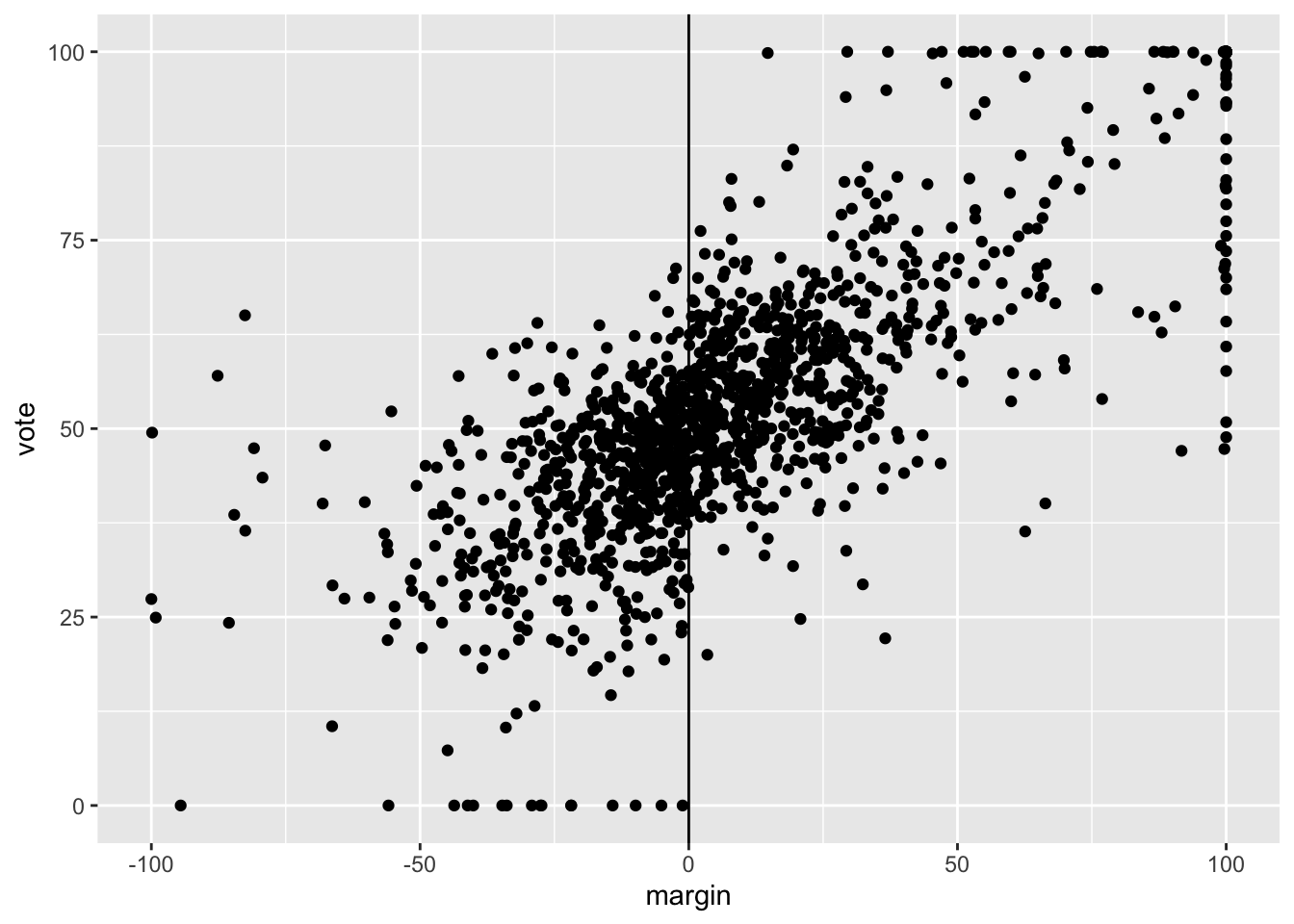
    • 選挙における現職効果（現在議席を得ている候補者のほうが選挙で有利になる）を推定

    • running variable \(=\) margin (前回の選挙におけるライバル政党との得票率差)

    • cutoff \(=\) 0 (差がない)

    • outcome variable \(=\) vote (選挙における得票率)

library(rdrobust)

library(tidyverse)

data("rdrobust_RDsenate")

raw <- rdrobust_RDsenate

7.3 Shap disconiniuity

  • 推計前に\(X\)と\(Y\)についての散布図を確認することを推奨
raw |> 
  ggplot(aes(x = margin,
             y = vote)
         ) +
  geom_point() +
  geom_vline(xintercept = 0)

  • 初期設定では2nd oder local polynominalを利用 (Gelman and Imbens (2019) の推奨)
Y <- raw$vote

X <- raw$margin

rdplot(y = Y,
       x = X)

  • 推定結果表 + 標準誤差
rdrobust(y = Y,
         x = X) |> 
  summary()
## Call: rdrobust
## 
## Number of Obs.                 1297
## BW type                       mserd
## Kernel                   Triangular
## VCE method                       NN
## 
## Number of Obs.                  595          702
## Eff. Number of Obs.             360          323
## Order est. (p)                    1            1
## Order bias  (q)                   2            2
## BW est. (h)                  17.754       17.754
## BW bias (b)                  28.028       28.028
## rho (h/b)                     0.633        0.633
## Unique Obs.                     595          665
## 
## =============================================================================
##         Method     Coef. Std. Err.         z     P>|z|      [ 95% C.I. ]       
## =============================================================================
##   Conventional     7.414     1.459     5.083     0.000     [4.555 , 10.273]    
##         Robust         -         -     4.311     0.000     [4.094 , 10.919]    
## =============================================================================

References

Calonico, Sebastian, Matias D. Cattaneo, Max H. Farrell, and Rocio Titiunik. 2021. Rdrobust: Robust Data-Driven Statistical Inference in Regression-Discontinuity Designs. https://CRAN.R-project.org/package=rdrobust.
Cattaneo, Matias D, Brigham R Frandsen, and Rocio Titiunik. 2015. “Randomization Inference in the Regression Discontinuity Design: An Application to Party Advantages in the US Senate.” Journal of Causal Inference 3 (1): 1–24.
Cattaneo, Matias D, Nicolás Idrobo, and Rocı́o Titiunik. 2019a. A Practical Introduction to Regression Discontinuity Designs: Extensions. Cambridge University Press.
———. 2019b. A Practical Introduction to Regression Discontinuity Designs: Foundations. Cambridge University Press.
Gelman, Andrew, and Guido Imbens. 2019. “Why High-Order Polynominals Should Not Be Used in Regression Discontinuity Designs.” Journal of Business and Econmomic Statistics 37 (3): 447–56.